python使用梯度下降和牛頓法尋找Rosenbrock函數最小值實例
Rosenbrock函數的定義如下:
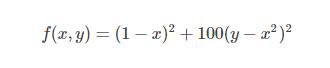
其函數圖像如下:
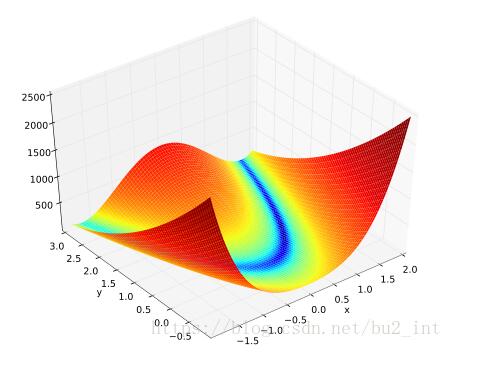
我分別使用梯度下降法和牛頓法做了尋找Rosenbrock函數的實驗。
梯度下降
梯度下降的更新公式:
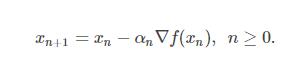
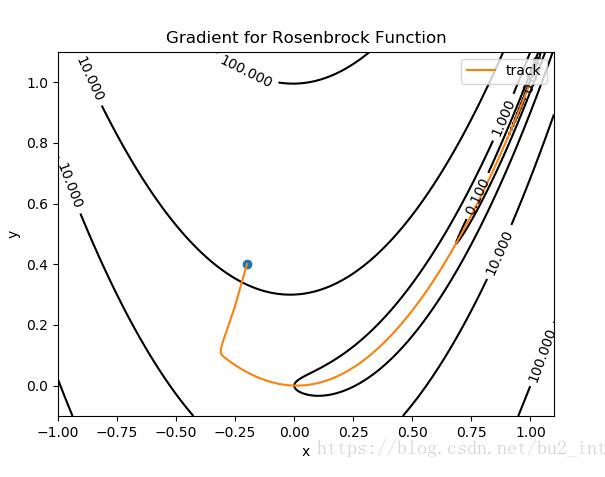
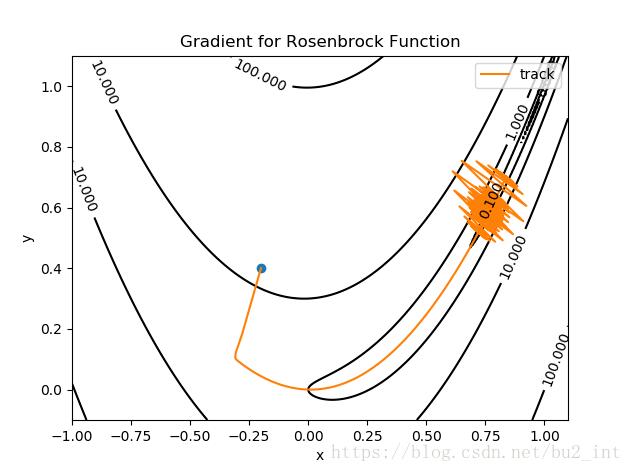
圖中藍色的點為起點,橙色的曲線(實際上是折線)是尋找最小值點的軌跡,終點(最小值點)為 (1,1)(1,1)。
梯度下降用了約5000次才找到最小值點。
我選擇的迭代步長 α=0.002α=0.002,αα 沒有辦法取的太大,當為0.003時就會發生振蕩:
牛頓法
牛頓法的更新公式:
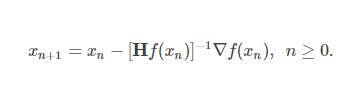
Hessian矩陣中的每一個二階偏導我是用手算算出來的。
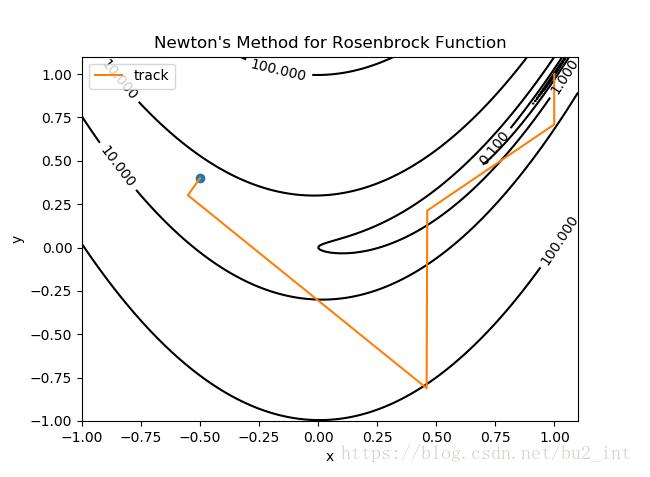
牛頓法只迭代了約5次就找到了函數的最小值點。
下面貼出兩個實驗的代碼。
梯度下降:
import numpy as npimport matplotlib.pyplot as pltfrom matplotlib import tickerdef f(x, y): return (1 - x) ** 2 + 100 * (y - x * x) ** 2def H(x, y): return np.matrix([[1200 * x * x - 400 * y + 2, -400 * x], [-400 * x, 200]])def grad(x, y): return np.matrix([[2 * x - 2 + 400 * x * (x * x - y)], [200 * (y - x * x)]])def delta_grad(x, y): g = grad(x, y) alpha = 0.002 delta = alpha * g return delta# ----- 繪制等高線 -----# 數據數目n = 256# 定義x, yx = np.linspace(-1, 1.1, n)y = np.linspace(-0.1, 1.1, n)# 生成網格數據X, Y = np.meshgrid(x, y)plt.figure()# 填充等高線的顏色, 8是等高線分為幾部分plt.contourf(X, Y, f(X, Y), 5, alpha=0, cmap=plt.cm.hot)# 繪制等高線C = plt.contour(X, Y, f(X, Y), 8, locator=ticker.LogLocator(), colors=’black’, linewidth=0.01)# 繪制等高線數據plt.clabel(C, inline=True, fontsize=10)# ---------------------x = np.matrix([[-0.2], [0.4]])tol = 0.00001xv = [x[0, 0]]yv = [x[1, 0]]plt.plot(x[0, 0], x[1, 0], marker=’o’)for t in range(6000): delta = delta_grad(x[0, 0], x[1, 0]) if abs(delta[0, 0]) < tol and abs(delta[1, 0]) < tol: break x = x - delta xv.append(x[0, 0]) yv.append(x[1, 0])plt.plot(xv, yv, label=’track’)# plt.plot(xv, yv, label=’track’, marker=’o’)plt.xlabel(’x’)plt.ylabel(’y’)plt.title(’Gradient for Rosenbrock Function’)plt.legend()plt.show()
牛頓法:
import numpy as npimport matplotlib.pyplot as pltfrom matplotlib import tickerdef f(x, y): return (1 - x) ** 2 + 100 * (y - x * x) ** 2def H(x, y): return np.matrix([[1200 * x * x - 400 * y + 2, -400 * x], [-400 * x, 200]])def grad(x, y): return np.matrix([[2 * x - 2 + 400 * x * (x * x - y)], [200 * (y - x * x)]])def delta_newton(x, y): alpha = 1.0 delta = alpha * H(x, y).I * grad(x, y) return delta# ----- 繪制等高線 -----# 數據數目n = 256# 定義x, yx = np.linspace(-1, 1.1, n)y = np.linspace(-1, 1.1, n)# 生成網格數據X, Y = np.meshgrid(x, y)plt.figure()# 填充等高線的顏色, 8是等高線分為幾部分plt.contourf(X, Y, f(X, Y), 5, alpha=0, cmap=plt.cm.hot)# 繪制等高線C = plt.contour(X, Y, f(X, Y), 8, locator=ticker.LogLocator(), colors=’black’, linewidth=0.01)# 繪制等高線數據plt.clabel(C, inline=True, fontsize=10)# ---------------------x = np.matrix([[-0.3], [0.4]])tol = 0.00001xv = [x[0, 0]]yv = [x[1, 0]]plt.plot(x[0, 0], x[1, 0], marker=’o’)for t in range(100): delta = delta_newton(x[0, 0], x[1, 0]) if abs(delta[0, 0]) < tol and abs(delta[1, 0]) < tol: break x = x - delta xv.append(x[0, 0]) yv.append(x[1, 0])plt.plot(xv, yv, label=’track’)# plt.plot(xv, yv, label=’track’, marker=’o’)plt.xlabel(’x’)plt.ylabel(’y’)plt.title(’Newton’s Method for Rosenbrock Function’)plt.legend()plt.show()
以上這篇python使用梯度下降和牛頓法尋找Rosenbrock函數最小值實例就是小編分享給大家的全部內容了,希望能給大家一個參考,也希望大家多多支持好吧啦網。
相關文章:
 網公網安備
網公網安備